Tỷ lệ vàng Fibonacci được ứng dụng và hình thành một trường phái đặc thù trong phân tích kỹ thuật chứng khoán thực chiến.
Fibonacci được ứng dụng rất nhiều từ Toán học, đến Mỹ thuật, và kể cả trong Kiến trúc.
Có nhiều cách ứng dụng Fibo trong phân tích chứng khoán như Fibonacci Retracement (hồi quy), Extension (Mở rộng), Time Extension (Thời gian mở rộng)…. Phổ biến nhất vẫn là Retracement để tìm điểm mua và cắt lỗ, Extension để xác định khả năng mở rộng xu hướng giúp có vùng chốt lời phù hợp.
Trong chuyên đề tìm hiểu và ứng dụng Fibonacci trong Phân tích kỹ thuật chứng khoán thực chiến, chúng ta sẽ cùng xem xét kỹ về cách dùng Fibonacci Retracement và Extension.
Nội dung
1. Fibonacci là ai?
Leonardo Pisano Bogollo (khoảng 1170 – khoảng 1250), còn được biết đến với tên Leonardo của Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, hay, phổ biến nhất, chỉ là Fibonacci, là một nhà toán học người Ý, được một số người xem là “nhà toán học tài ba nhất thời Trung Cổ”.

Ông đã có một khoảnh khắc “Aha!” xuất thần Khi ông phát hiện ra một loạt các con số đơn giản tạo ra các tỷ lệ mô tả tỷ lệ tự nhiên của những thứ trong vũ trụ.
Leonardo sinh ra ở Pisa. Cha ông, Guglielmo, có biệt danh Bonaccio (“hiền hậu” hoặc “đơn giản”). Mẹ của Leonardo, Alessandra, mất khi ông được chín tuổi. Leonardo sau khi chết được gọi là Fibonacci (lấy từ filius Bonacci, nghĩa là con của Bonaccio).
Guglielmo làm giám đốc một cơ sở thương mại (theo một số người ông làm cố vấn cho Pisa) ở Bugia, một hải cảng ở phía đông Algiers ở vương quốc hồi giáo Almohad ở Bắc Phi (giờ là Bejaia, Algérie). Khi còn là một cậu bé, Leonardo đã đi đến đó để giúp cha mình. Đây là nơi ông đã học Chữ số Ả Rập.
Nhận ra rằng số học với Chữ số Ả Rập đơn giản hơn và hiệu quả hơn chữ số La Mã, Fibonacci đã đi du lịch khắp thế giới, Địa Trung Hải để học theo những nhà toán học hàng đầu Ả Rập vào thời đó. Leonardo trở về sau chuyến du lịch vào khoảng năm 1200. Vào năm 1202, vào tuổi 32, ông phát hành cuốn Liber Abaci (Sách tính), và từ đó đã giới thiệu Chữ số Ả Rập cho châu Âu.
Leonardo trở thành vị khách thường xuyên của Hoàng đế Frederick II, người rất thích toán học và khoa học. Năm 1225, vị hoàng đế cùng một số nhà toán học đã thử tài ông bằng bài toán sau: “Tìm Số hữu tỉ x sao cho x-mũ-2 + 5 và x-mũ-2 – 5 đều là bình phương của các số hữu tỉ. Sau khi suy nghĩ, Fibonacci đã tìm ra, số đó là 41/12. Đến nay, chưa ai tìm ra chính xác ông đã tìm bằng cách nào. Vào năm 1240, Cộng hòa Pisa vinh danh Leonardo, được biết đến với tên Leonardo Bigollo, bằng cách trao lương cho ông.
Vào thế kỷ thứ 19, một bức tượng của ông được tạc ở Pisa. Ngày nay nó nằm ở hành lang của nghĩa trang lịch sử Camposanto ở Piazza dei Miracoli.
2. Quy tắc hình thành chuỗi số Fibonacci
Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1 hoặc 1 và 1, các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng hai phần tử trước nó.
Công thức truy hồi của dãy Fibonacci:
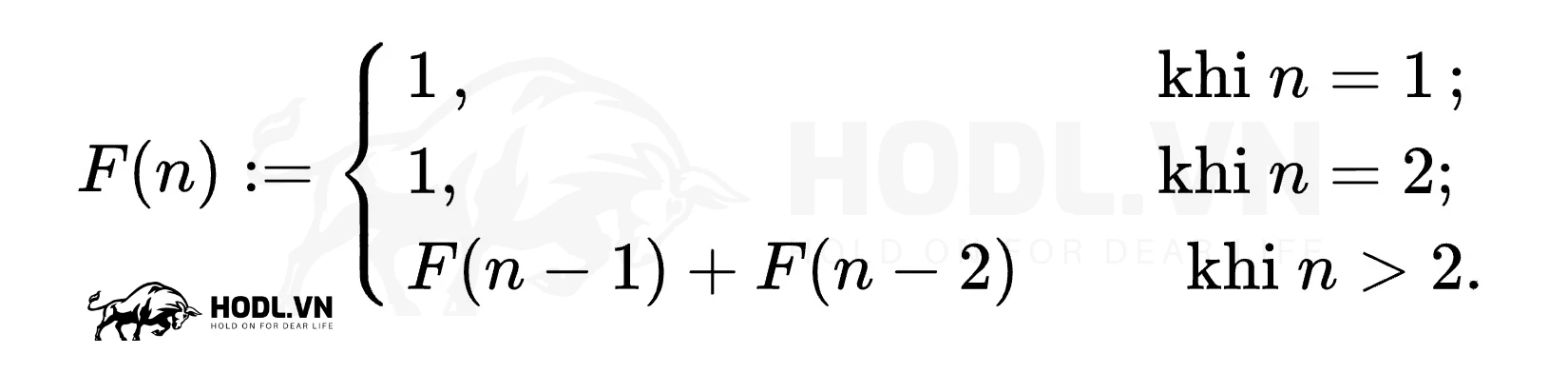
Các con số đầu tiên của chuỗi Fibonacci: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
| n | F(n) | n | F(n) | n | F(n) |
|---|---|---|---|---|---|
| n | F(n) | n | F(n) | ||
| 0 | 0 | 1 | 1 | 2 | 1 |
| 3 | 2 | 4 | 3 | 5 | 5 |
| 6 | 8 | 7 | 13 | 8 | 21 |
| 9 | 34 | 10 | 55 | 11 | 89 |
| 12 | 144 | 13 | 233 | 14 | 377 |
| 15 | 610 | 16 | 987 | 17 | 1.597 |
| 18 | 2.584 | 19 | 4.181 | 20 | 6.765 |
| 21 | 10.946 | 22 | 17.711 | 23 | 28.657 |
| 24 | 46.368 | 25 | 75.025 | 26 | 121.393 |
| 27 | 196.418 | 28 | 317.811 | 29 | 514.229 |
| 30 | 832.040 | 31 | 1.346.269 | 32 | 2.178.309 |
| 33 | 3.524.578 | 34 | 5.702.887 | 35 | 9.227.465 |
| 36 | 14.930.352 | 37 | 24.157.817 | 38 | 39.088.169 |
Các con số này được tính như sau:
- Số đầu tiên bắt đầu bằng 0
- Số thứ hai bắt đầu bằng 1
- Số thứ ba = Số đầu tiên + Số thứ 2 = 0 + 1 = 1
- Số thứ tư = Số thứ 2 + Số thứ 3 = 1 + 1 = 2
- Số thứ năm = Số thứ 3 + Số thứ 4 = 1 + 2 = 3.
- Số thứ sáu = Số thứ 4 + Số thứ 5 = 2 + 3 = 5….
3. Quan hệ với Tỷ lệ vàng φ (phi)
Tỷ lệ vàng φ (phi), được đinh nghĩa là tỷ số khi chia đoạn thẳng thành hai phần sao cho tỷ lệ giữa cả đoạn ban đầu với đoạn lớn hơn bằng tỷ số giữa đoạn lớn và đoạn nhỏ.
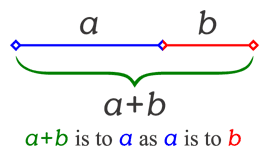
Có thể chứng minh rằng nếu quy độ dài đoạn lớn về đơn vị thì tỷ lệ này là nghiệm dương của phương trình:

Tỷ lệ 0.618: Sau một vài số đầu tiên trong chuỗi Fibonacci, nếu bạn lấy một số bất kỳ chia cho số ngay sau nó, bạn sẽ nhận được 0.618. Ví dụ, 34 chia cho 55 bằng 0.618.
Tỷ lệ 0.382: Trong 03 số liền kề thuộc dãy Fibonacci, Ví dụ: 34, 55, 89 nếu bạn lấy số đầu tiên chia cho số thứ 3, chính là 34/89 bạn sẽ được 0.382.
Các con số trong dãy này cứ liên tục lặp lại trong suốt dãy như vậy.
Để hiểu rõ hơn:
Giờ chúng ta sẽ tìm số tiếp theo của Dãy Fibonacci đứng sau số 89, chính là = 55+89 = 144.
Ta cũng thấy tiếp tục rằng:
- 55/89 = 0.618
- 55/144 = 0.382.
Thật tuyệt vời phải không?
Các tỷ lệ này được gọi là “trung bình vàng”. Ok, chúng ta chỉ hiểu đến đây thôi, bạn không cần hiểu quá nhiều.
4. Các tỷ lệ Fibonacci buộc phải biết trong chứng khoán
Bạn sẽ không thực sự cần phải biết cách tính tất cả các tỷ lệ này. Các nền tảng phân tích từ các Brokers hoặc các công cụ phân tích kỹ thuật cổ phiếu như Amibroker, MetaStocks đều hỗ trợ bạn xác định và tính toán các tỷ lệ này ra con số chính xác trên biểu đồ.
Tuy nhiên, bạn vẫn cần phải biết các lý thuyết cơ bản đằng sau các tỷ lệ vàng này để có thể ứng dụng hoàn hảo trong phân tích biểu đồ Forex và hỗ trợ tìm kiếm điểm vào lệnh phù hợp, hiệu quả.
4.1 Fibonacci Retracement
Dưới đây là danh sách các mức Fibonacci hồi quy phổ biến được sử dụng trong phân tích kỹ thuật theo từng trường phái:
Các Mức Fibonacci Retracement phổ biến
- 0.236 – 23.6%
- 0.382 – 38.2%
- 0.500 – 50.0%
- 0.618 – 61.8%
- 0.786 – 78.6%
Mức Fibonacci Retracement theo lý thuyết Dow
- 0.33 – 33%
- 0.50 – 50.0%
- 0.66 – 66%
Các nhà giao dịch sử dụng các mức Fibonacci Retracement như các vùng hỗ trợ và kháng cự tiềm năng. Trong đó tỷ lệ 38.2%, 50.0%, 61.8% được sử dụng nhiều nhất. Tỷ lệ 78.6% thường được sử dụng cho các mô hình giá điều hoà.
Mục đích sử dụng các Mức Fibonacci Retracement của các Nhà đầu tư:
- Xác định điểm vào lệnh
- Xác định điểm Stop Loss (Cut lỗ)
- Xác định vùng Kháng cự và Hỗ trợ mạnh.
Hầu hết các nhà giao dịch sử dụng các mức Fibonacci Retracement với các mục đích trên, nên Tỷ lệ vàng này có xu hướng tương tự như Lời tiên trị tự đúng.
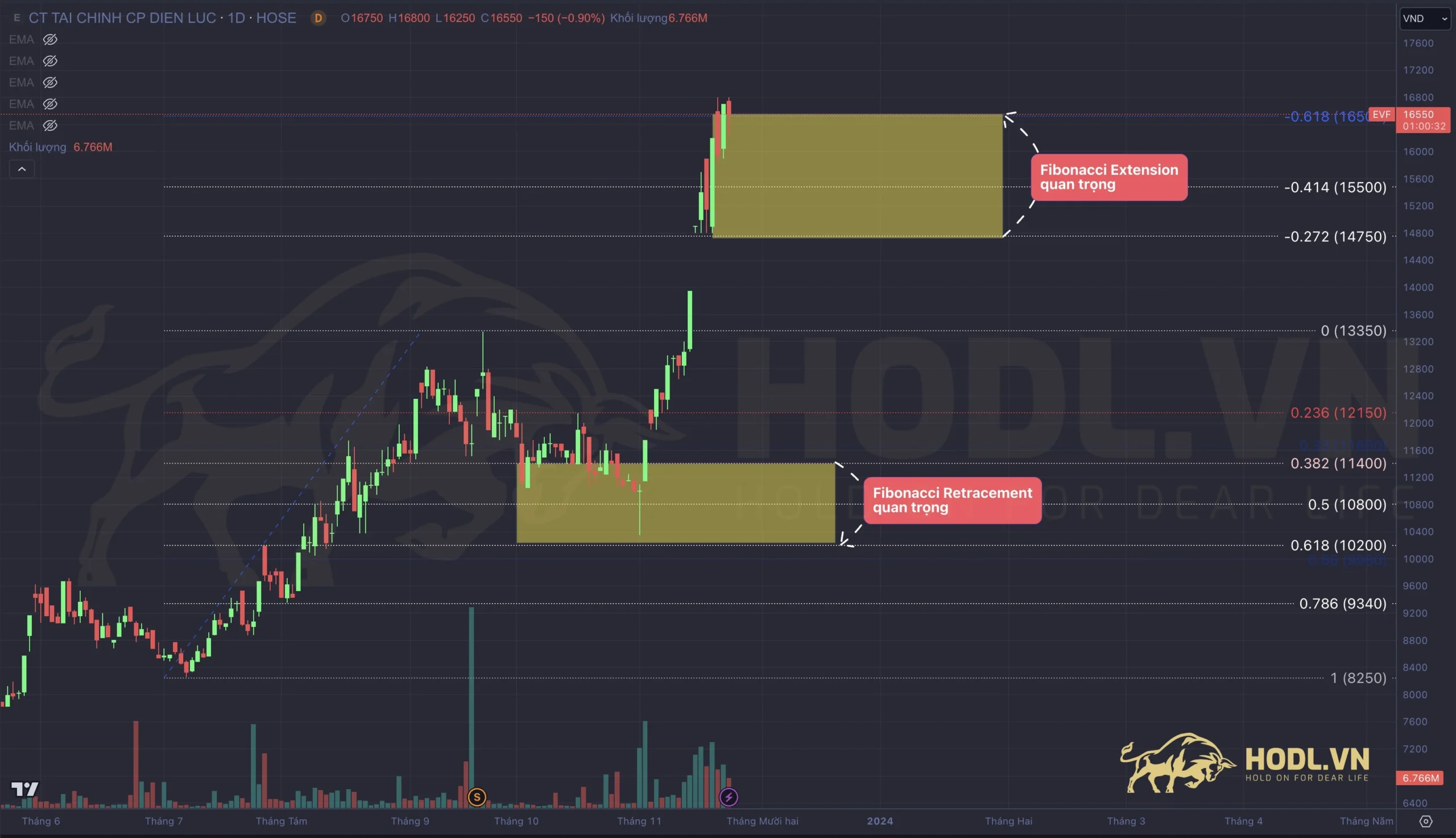
4.2 Fibonacci Extension
Các mức Fibonacci Extension:
- 1.272 – 127.2%
- 1.414 – 141.4%
- 1.618 – 161.8%
Các nhà giao dịch sử dụng các mức Fibonacci Extension (Fibonacci Mở rộng) như các mức chốt lời – Take Profit và tìm kiếm vùng có khả năng mở rộng xu hướng của giá cổ phiếu.
Fibonacci Extension cũng được nhiều nhà giao dịch đang theo dõi các mức này để đặt lệnh mua và bán, chốt lời, công cụ này có xu hướng diễn ra khá chính xác nhưng nó không hoàn toàn đúng và cũng không có xu hướng giống như Hiệu ứng lời tiên tri tự đúng.
5. Tổng kết
Trên đây là tất cả lý thuyết về Fibonacci trong phân tích kỹ thuật và giao dịch chứng khoán. Dãy số Fibonacci được ứng dụng rộng rãi trong rất nhiều lĩnh vực không chỉ giới hạn trong đầu tư tài chính như:
- Nhiếp ảnh
- Hội hoạ
- Kiến trúc
- Toán học
- …
Trong chuyên đề về Fibonacci trên HODL.VN, chúng ta sẽ chỉ tìm hiểu cách ứng dụng dãy số Fibonacci trong phân tích kỹ thuật biến động giá các chỉ số chứng khoán và cổ phiếu phục vụ cho mục đích đầu tư.
Cách ứng dụng Fibonacci Retracement và Fibonacci Extension chi tiết sẽ được cập nhật trong các bài viết tiếp theo.
Chúc các bạn giao dịch thành công!